Revisiting the question of "Has global warming stopped since 1998?"—again.
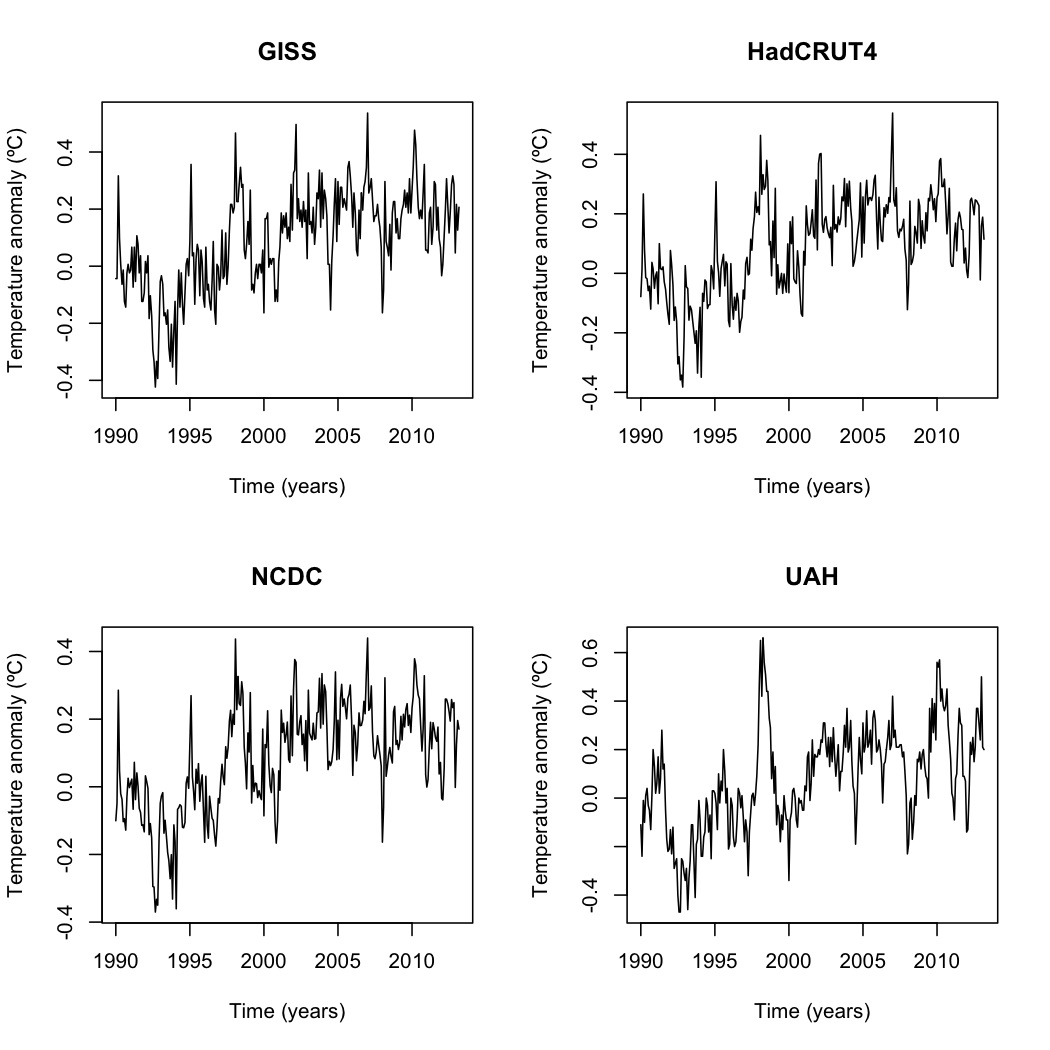
Let me be blunt: There is little evidence that global warming stopped in 1998 or any year thereafter. Most of the evidence we have, from the energy imbalance to total heat content to ocean heat content, show that global warming continues, as I previously explained here , here , and here . The only piece of evidence that appears to show that global warming has stopped is that the trend in surface temperature data is not statistically significant in recent years. However, that is at best ambiguous. No significant trend could mean that warming continues but short-term variation in the data masks the trend, that there's no warming or that there's a cooling trend but not enough data for that to be significant. There's no real way to tell unless you either a) add enough data for short-term variation to cancel out or b) use statistical techniques to factor out the known natural variation. In this article, I expand on my previous analyses of surface temperature, ...