How we know global warming is because of CO2: Part 1
The existence of Earth's greenhouse effect was first postulated by Joseph Fourier in the 1820s, when he calculated that the Earth should be much colder than it actually is. Using the Stefan-Boltzmann law, and modern measurements, we can calculate what that temperature should be. The equation for doing so is
where
S = solar energy received by the planet (W/m2),
A = albedo, which is the fraction of S that is reflected back into space by snow, ice, sulphate aerosols, etc,
ε = emissivity, which is the fraction of heat energy emitted from the surface that escapes into space, and
σ = Stefan-Boltzmann constant (5.6704 x 10-8 W/m2/K4).
S has been measured via satellites since November 1978. The average is 1,366 W/m2, although it has declined slightly by -0.645 W/m2 over that time:
Albedo has also been measured via satellite, with an average of 0.30. In contrast with solar output, albedo, however, has remained roughly the same, with little to no trend over the time period 1983-2006 (graph from NASA ISCCP):
You can clearly see the brief spikes in albedo due to sulfate aerosols from the eruptions of El Chichón in 1982 and Mount Pinatubo in 1991 but no real change otherwise.
Emissivity for the surface of the Earth ranges from 0.965 up to 0.995 for seawater (data from ICESS) and 0.90 up to 0.97 for terrestrial surfaces (Jin and Liang 2006). The average for the entire surface is around 0.98, given that the oceans are 71% of the Earth's surface. That emissivity would hold for the entire Earth if there was no greenhouse effect.
The numerator S*(1-A) gives us the amount of the sun's energy that actually makes it to the Earth's surface and is absorbed by the surface. That absorbed energy is then reradiated as heat. The denominator 4εσ gives us the amount of that heat that makes it out to space. Plugging the values for S, A, and ε into the Stefan-Boltzmann law gives us the expected temperature of the Earth's surface without a greenhouse effect:
For those readers in the US, that's 1.31ºF. That's cold. The actual average temperature of the Earth's surface over the past 10 years? A relatively balmy 14.58ºC (58.24ºF) according to NASA GISS. The effective emissivity needed to achieve that global surface temperature is 0.615. That means that gases in the atmosphere are reducing emissivity by 0.365. And since emissivity is a measure of how much heat is escaping, the gases that create the greenhouse effect must be absorbing heat, preventing it from escaping into space and keeping it in the atmosphere.



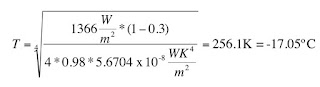



Comments
Post a Comment